PRESENTACION
ANGIE VALENTINA MAZO ESCOBAR 9°01
En este blog encontraras recursos para aprender la solucion de determinantes. para esto utilizaremos Explicacion del tema, Videos, Ejemplos, Imagenes y otros tipos de enlaces que explicaran el tema.
EXPLICACION DEL TEMA
Historia de los determinantes
Los determinantes fueron introducidos en Occidente a partir del siglo XVI, esto es, antes que las matrices, que no aparecieron hasta el siglo XIX. Conviene recordar que los chinos (Hui, Liu. iuzhang Suanshu o Los nueve capítulos del arte matemático. ) fueron los primeros en utilizar la tabla de ceros y en aplicar un algoritmo que, desde el Siglo XIX, se conoce con el nombre de Eliminación de Gauss-Jordan.
La historia de los determinantes
Los determinantes hicieron su aparición en las matemáticas más de un siglo antes que las matrices. El término matriz fue creado por James Joseph Sylvester, tratando de dar a entender que era “la madre de los determinantes”.
Algunos de los más grandes matemáticos de los siglos XVIII y XIX contribuyeron al desarrollo de las propiedades de los determinantes. La mayoría de los historiadores coinciden en afirmar que la teoría de los determinantes se originó con el matemático alemán Goofried Wilhelm Leibniz (1646-1716) quien fue con Newton, el co inventor del cálculo diferencial e integral. Leibniz empleó los determinantes en 1693 con relación a los sistemas de ecuaciones lineales simultáneas. No obstante hay quienes creen que el matemático japonés Seki Kowa hizo lo mismo unos 10 años antes.
Las contribuciones más prolíficas a la teoría de los determinantes fueron las del matemático francés Agustin-Louis Cauchy (1789-1857). Cauchy escribió, en 1812 una memoria de 84 páginas que contenía la primera demostración del teorema detAB=detA detB. En 1840 Cauchy hizo muchas otras contribuciones a las matemáticas. En su texto de cálculo de 1829 Lecons sur le calcul différential, dio la primera definición razonablemente clara de límite.
Cauchy escribió ampliamente tanto en las matemáticas puras como en las aplicadas. Solo Euler escribió más. Cauchy hizo contribuciones en varias áreas, incluyendo la teoría de las funciones reales y complejas, la teoría de la probabilidad, geometría, teoría de propagación de las ondas y las series infinitas.
Hay algunos otros matemáticos que merecen ser mencionados aquí. El desarrollo de un determinante por cofactores fue empleado por primera vez por el matemático francés Pierre de Laplace (1749-1827). Laplace es mejor conocido por la transformación que lleva su nombre que se estudia en los cursos de matemáticas aplicadas.
Métodos de cálculo
Para el cálculo de determinantes de matrices de cualquier orden, existe una regla recursiva (teorema de Laplace) que reduce el cálculo a sumas y restas de varios determinantes de un orden inferior. Este proceso se puede repetir tantas veces como sea necesario hasta reducir el problema al cálculo de múltiples determinantes de orden tan pequeño como se quiera. Sabiendo que el determinante de un escalar es el propio escalar, es posible calcular el determinante de cualquier matriz aplicando dicho teorema.
Además de esta regla, para calcular determinantes de matrices de cualquier orden podemos usar otra definición de determinante conocida como Fórmula de Leibniz.
La fórmula de Leibniz para el determinante de una matriz cuadrada A de orden n es:
donde la suma se calcula sobre todas las permutaciónes σ del conjunto {1,2,...,n}. La posición del elemento i después de la permutación σ se denota como σi. El conjunto de todas las permutaciones es Pn. Para cada σ, sgn(σ) es la signatura de σ, esto es +1 si la permutación es par y −1 si es impar (ver Paridad de permutaciones).
En cualquiera de los n! sumandos, el término
denota el producto de las entradas en la posición (i, σi), donde i va desde 1 hasta n:
[editar] Matrices de orden inferior
El caso de matrices de orden inferior (orden 1, 2 ó 3) es tan sencillo que su determinante se calcula con sencillas reglas conocidas. Dichas reglas son también deducibles del teorema de Laplace.
Una matriz de orden uno, es un caso trivial, pero lo trataremos para completar todos los casos. Una matriz de orden uno puede ser tratada como un escalar, pero aquí la consideraremos una matriz cuadrada de orden uno:
El valor del determinante es igual al único termino de la matriz:
Los determinantes de una matriz de orden 2:
se calculan con la siguiente fórmula:
Dada una matriz de orden 3:
En determinante de orden 3 se calcula mediante la regla de Sarrus:
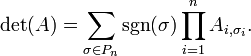
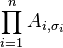



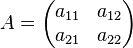





No hay comentarios:
Publicar un comentario